The BusPlus Project
Connecting people
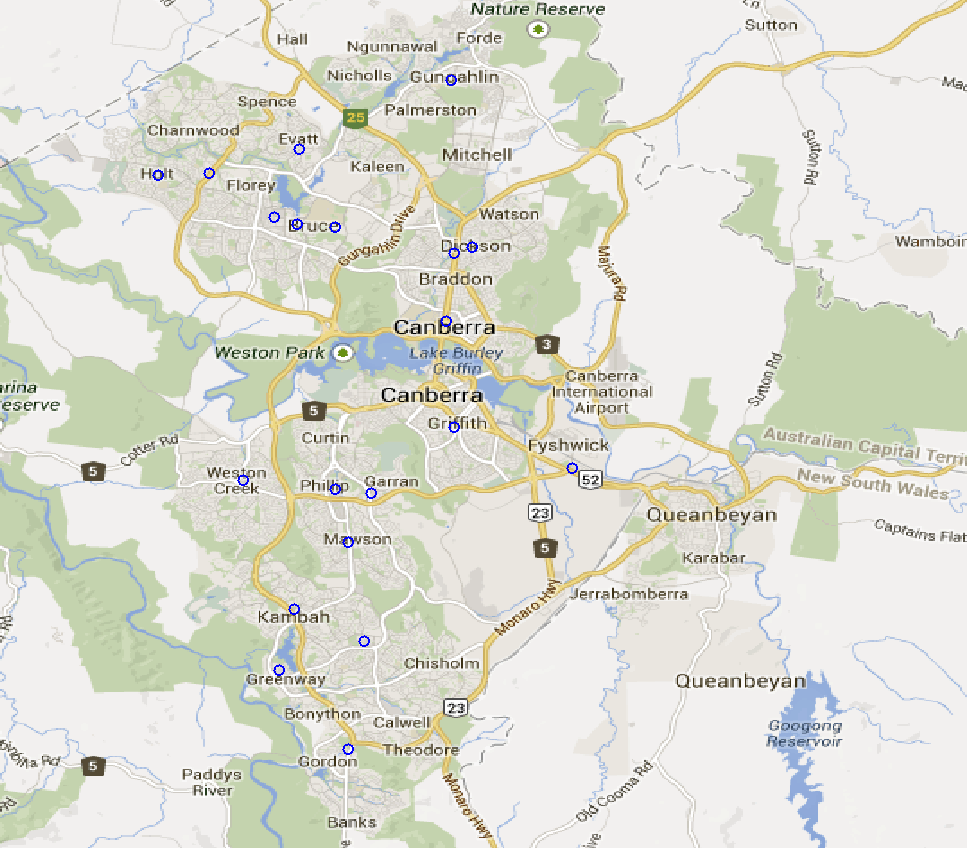
Canberra was founded in 1913 by American architect Walter Burley Griffin, it is a vast, planned city built as a collection of towns separated by green belts.
- Canberra: 381,488 hab.
814.2 km² (428.6/km²) - Montréal (City): 1,649,519 hab.
431.50 km² (4,517.6/km²) - Montréal (Metro): 4,127,100 hab.
4,258.31 km² (898.1/km²)
Why BusPlus?
Canberra suffers heavily from low patronage
Action
- Demand is too spread out
- Most buses run almost empty
- Very high cost: almost 100 bus lines
- Service is not regular, esp. off-peak
BusPlus
- Booking system, trips start at a bus stop
- Low waiting time (15min preparation time)
- High frequency buses (aiming for every 15min)
- Shuttles for "first" and "last mile"
Modelling BusPlus
Public transportation network design
Modelling BusPlus
The data
- One week of data (Monday to Saturday)
- 2,800 bus stops
- 21,000 trips for 60,000 passengers
- Two sets of hubs: $H_{10}$ and $H_{20}$
Modelling BusPlus
Hub Location and BusPlus
The Hub-Arc Location Problem [1] (HALP) is a variant of the well-known Hub Location Problem where hubs do not form a complete graph.
Modelling BusPlus
Hub Location and BusPlus
The Hub-Arc Location Problem [1] (HALP) is a variant of the well-known Hub Location Problem where hubs do not form a complete graph.
Modelling BusPlus
Hub Location and BusPlus
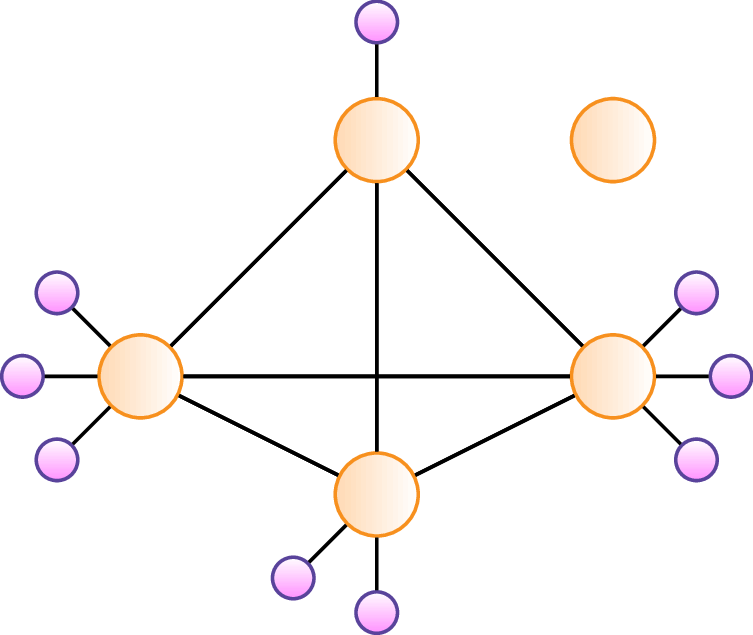
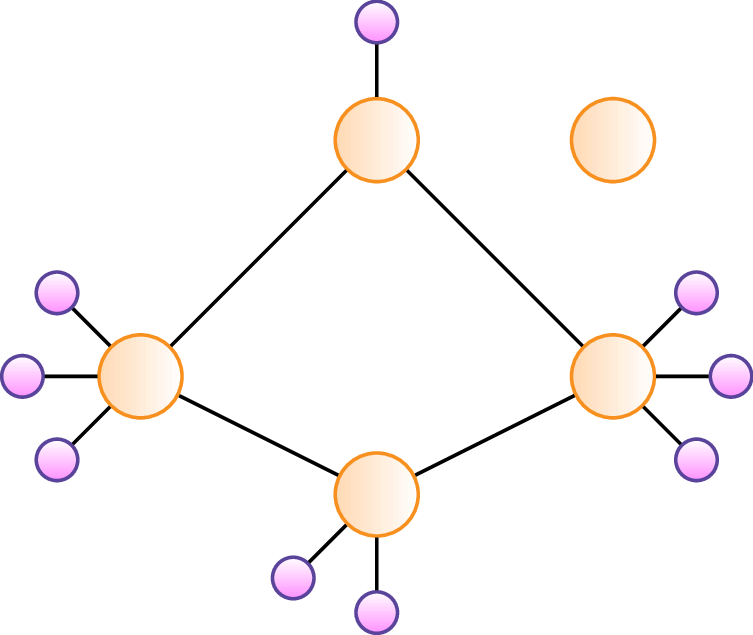
The Hub-Arc Location Problem [1] (HALP) is a variant of the well-known Hub Location Problem where hubs do not form a complete graph.
The HALP is used when designing networks where opening links between hubs has a cost but these links provide economies of scale (e.g., transhipping networks).
Modelling BusPlus
Variables and costs
- Costs is a mix of expenses and time, conversion factor $\alpha$
- Taxis $x$ available everywhere to route trips, combination of time and cost: $$\tau = (1 - \alpha) d_{ij} \cdot T + \alpha \cdot t_{ij}$$
- Bus legs (hub arcs) $z$ with a fixed installation cost: $$\beta = (1 - \alpha) d_{hl} \cdot B$$
- Bus trips $y$ between hubs, only cost $$\gamma = \alpha (t_{ij} + S)$$
Modelling BusPlus
Hub-and-Shuttle Public Transportation System (HSPTS)
$$
\begin{align}
\min && \sum_{r \in T} \sum_{i,j \in N} \tau_{ij}^r x_{ij}^r + \sum_{r \in T}\sum_{h, l \in H} \gamma_{hl}^r y^r_{hl} & + \sum_{h,l \in H} \beta_{hl} z_{hl} \\
s.t. && \sum_{l \in H} z_{hl} & = \sum_{l\in H} z_{lh} & \forall h \in H \label{eq:hub} \\
& & y^r_{hl} & \leq z_{hl} & \forall r\in T, \forall h,l \in H \label{eq:hard} \\
& & \sum_{j \in N} \left( x^r_{ij} - x^r_{ji} \right) + \sum_{\substack{h \in H \\ \text{if } i \in H}} \left(y^r_{ih} - y^r_{hi} \right) & = 1, 0, -1 & \forall r \in T, \forall i \in N \\
& & x_{ij}^r, y_{hl}^r \geq 0; z_{hl} \in \B
\end{align}
$$
Trimming the Model
A million variables is just too much!
Trimming the Model
Warming up, because not all taxis are born equal...
T-Filtering
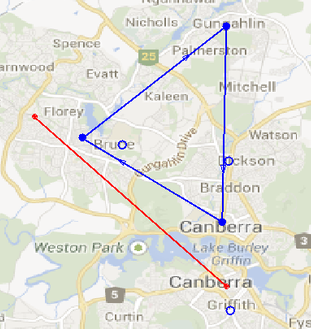
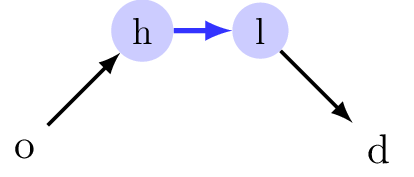
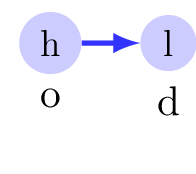
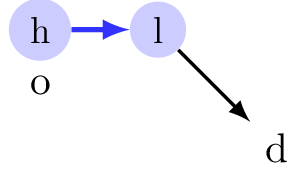
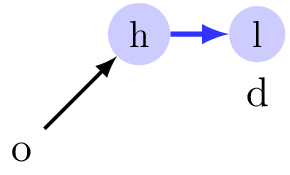
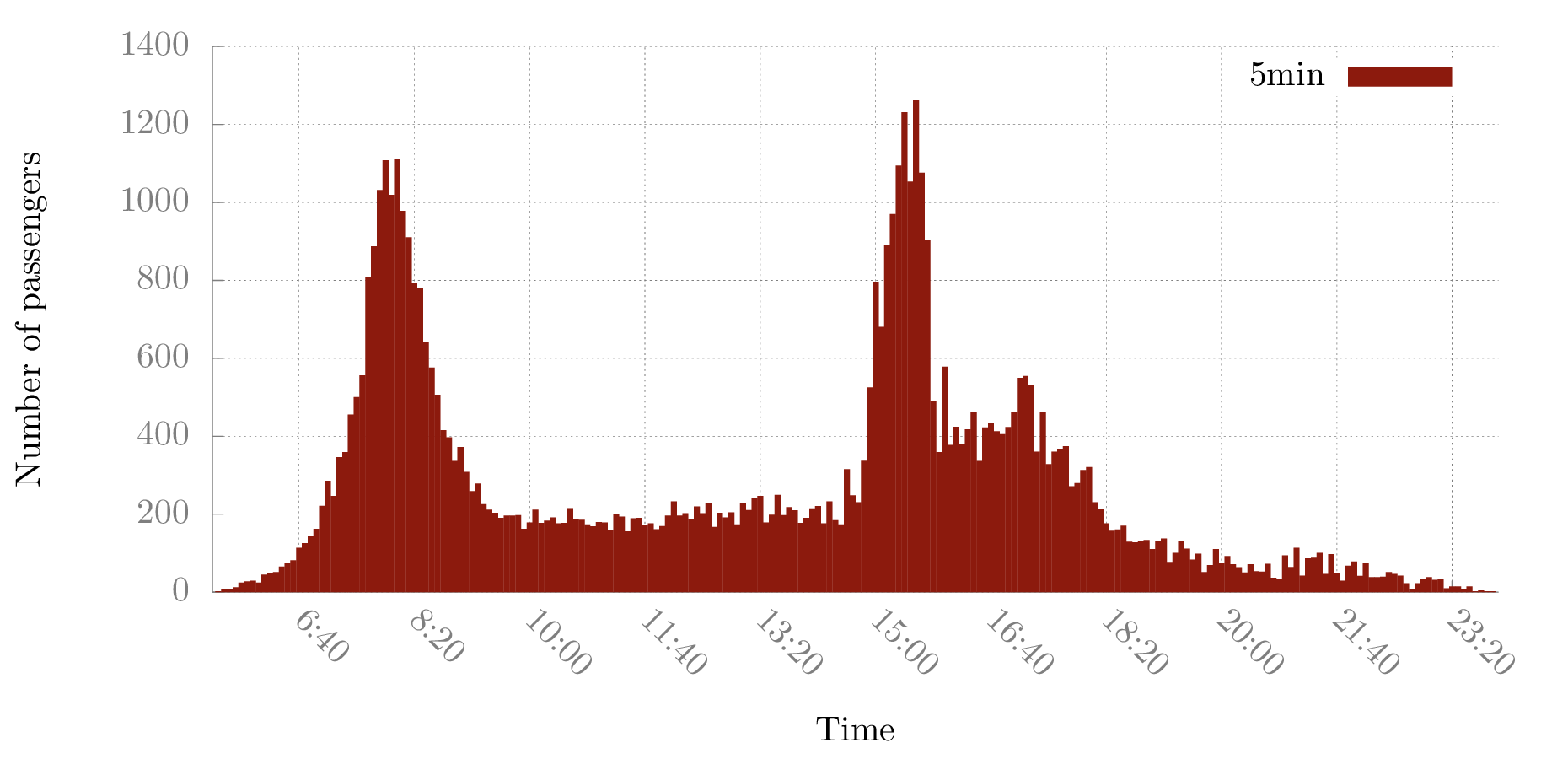
Some trips will never use the bus network, whatever the configuration!
About 30% of trips can just be omitted in the model when using 10 hubs; 20% with 20 hubs.
L-Filtering
We have an upper bound on the cost $\tau_{od}$, let us remove any "best" scenario above that:
if $\tau_{oh} + \gamma_{hl} + \tau_{ld} > \tau_{od}$, then remove $x_{oh}$ and $x_{ld}$.
55% to 58% reduction in the number of $x$ variables.
$H_{10}$ has 130,000 $x$ variables, $H_{20}$ has 300,000.
Benders Decomposition
A short introduction
Benders Decomposition
What is it?
- Take a MIP
- Project out continuous variables
- You obtain two problems: a master and a sub-problem
BusPlus
The HALP can actually be seen as a two-level decision process.
- 1. Which arcs to open
- 2. How to route the flow
Benders Decomposition
How does it work?
- The master is a relaxed problem, it fixes the integer variables
- Solve the dual LP with the candidate solution to generate cuts
- Instead of having to explore all solutions, only add "relevant" constraints
Benders Decomposition
Some more maths
Master
$$ \begin{align} \min && \sum_{h,l \in H} \beta_{hl} z_{hl} + q \nonumber \\ s.t. && \sum_{l \in H} z_{hl} = \sum_{l \in H} z_{lh} &\ \forall h \in H \\ && \text{A set of cuts}\\ && z \in \B, q \in \R \end{align} $$Sub-Problem
$$ \begin{align} \min && \sum_{r \in T} \left( \sum_{i, j \in N}% \tau_{ij}^r x_{ij}^r +% \sum_{h, l \in H} \gamma_{hl}^r y_{hl}^r \right) \\ s.t. && y^r_{hl} \leq \bar{z}_{hl} \quad \forall r \in T, h,l \in H\\ && \sum_{j \in N} \left( x^r_{ij} - x^r_{ji} \right) + \sum_{\substack{h \in H \\ \text{if } i \in H}} \left(y^r_{ih} - y^r_{hi} \right) = 1, 0, -1 \\ && \forall r \in T, \forall i \in N \\ && 0 \leq x_{ij}^r, y_{hl}^r \leq 1 \end{align} $$Benders Decomposition
Some more maths
Master
$$ \begin{align} \min\quad \sum_{h,l \in H} \beta_{hl} z_{hl} + q \nonumber \\ s.t.\quad \sum_{l \in H} z_{hl} = \sum_{l \in H} z_{lh} &\quad \forall h \in H \\ u_o - u_d - \sum_{h, l \in H} z_{hl} v_{hl} \geq q &\quad\! \forall (u, v) \in \mathcal{O} \\ z \in \B, q \in \R \end{align} $$(Independent) Dual Sub-Problem
$$
\begin{align}
\max && u_o - u_d - \sum_{h, l \in H} & \bar{z}_{hl} v_{hl} \\
s.t. && u_i - u_i & \leq \tau_{ij} & \forall i,j \in N \\
&& u_h - u_l - v_{hl} & \leq \gamma_{hl} & \forall h,l \in H \\
&& u, v \geq 0
\end{align}
$$
Improving Benders
There is no free lunch!
Improving Benders
Pareto optimal cuts [2]
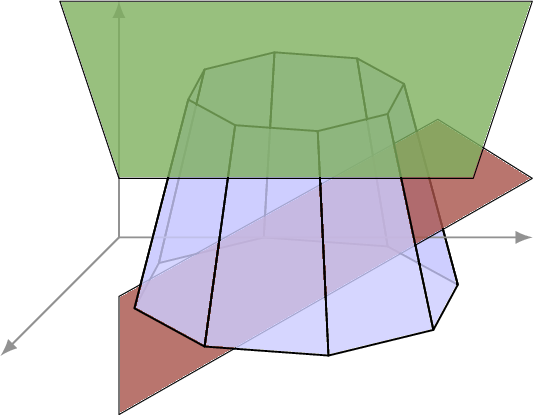
One issue with min-cost flow, as with many "network" problems, is its high degeneracy: multiple equivalent optimal solutions.
So we design a Pareto optimal sub-problem.
- Modify the objective function using a core point
- Add a constraint to restrict the solution space with the solution of the primal problem
$$
\begin{align}
\max && u_o - u_d - \sum_{h,l \in H} & z^0_{hl} v_{hl} \\
s.t. && u_i- u_j & \leq \tau_{ij} \quad \forall i,j \in D^r \\
&& u_h - u_l - v_{hl} & \leq \gamma_{hl} \quad \forall h, l \in H \\
&& u_o - u_d - \sum_{h,l \in H} \bar{z}_{hl} v_{hl} &= spp(o, d, \bar{Z}) \\%
&& u \geq 0, v \geq 0
\end{align}
$$
Improving Benders
Pareto optimal cuts and independent sub-problems
Improving Benders
Cut bundling
With fixed $z$, the sub-problem becomes a collection of independent min-cost flows.
We need to decide how we are going to "bundle" the cuts.
- All in one
- By origin
- By leg used
- By closest hub
- One per trip
Improving Benders
Core point update
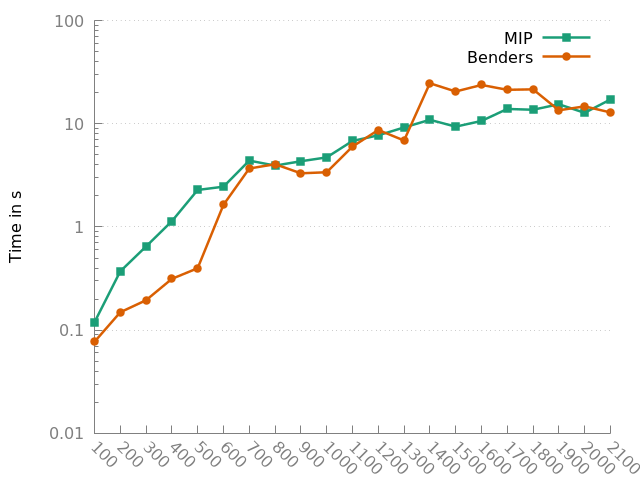
Papadakos [3] showed that the choice of a core point can dramatically influence the performance of Pareto approach. Even better when updating it. $$ z^{0 (n + 1)}_{hl} = \frac{z^{0 (n)}_{hl} + \bar{z}^{(n)}_{hl}}{2} $$
Results
... or "Was it all worth it?"
Results
Benders vs. MIP (small)
Results
Benders vs. MIP (large)
Results
Sensitivity analysis
Results $H_{10}$
Results $H_{20}$
Questions?
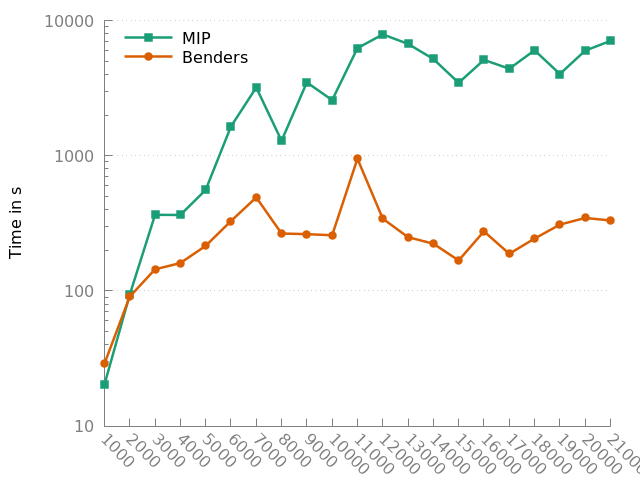
Thank you for your attention.
Paper available
arXiv:1601.00367 [cs.AI]